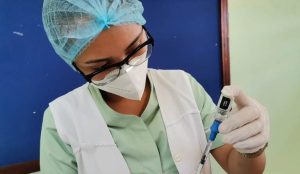
Paul Erdős, el extraordinario genio matemático que nunca tuvo posesiones ni aprendió a cortar en dos una toronja

Si hubieras conocido a Paul Erdős cuando tenía 4 o 5 años, te habría preguntado la fecha y hora de tu nacimiento para calcular mentalmente cuántos segundos habías vivido.
Si lo hubieras conocido dos o tres años más tarde, te habría dado la solución a algún problema que se hubiera inventado, como cuánto tiempo te tomaría llegar al Sol en tren.
Pero si le hubieras pedido a los 14 años que se amarrara los cordones de los zapatos, no habría sabido cómo hacerlo.
No era lo único que no sabía hacer.
«Recuerdo claramente, acababa de ir a Inglaterra a estudiar. Era la hora del té y sirvieron pan. Me daba mucha vergüenza admitir que nunca había untado un trozo de pan con mantequilla«.
Tenía 21 años de edad.

Al final, se animó a intentarlo. «No fue tan difícil», contó años después.
La razón de tal discordancia está en las circunstancias de su nacimiento. Ocurrió el mismo día de 1913 en Hungría en el que sus dos hermanas, de 3 y 5 años de edad, murieron de escarlatina.
Su padre, poco después del estallido de la Primera Guerra Mundial, fue hecho prisionero por los rusos y regresó a casa desde Siberia solo seis años más tarde.
Su madre, aterrada de que su precioso hijo contrajera una enfermedad fatal, prefirió educarlo en casa, con la ayuda de una institutriz, y se dedicó a mimarlo y protegerlo de los problemas cotidianos.
Ambos padres eran profesores de matemáticas y, leyendo los libros que tenían en casa, Erdős se enamoró de los números desde temprana edad.
«Eran mis amigos. Podía depender de que siempre estarían ahí y siempre se comportarían de la misma manera», recordaba cuando ya era el legendario matemático en el que se convirtió.
Es por eso que antes de aprender a untarle mantequilla al pan, Erdős publicó su primer artículo académico.
«No fue publicado a una edad fenomenalmente temprana como la de otros niños prodigios húngaros que vinieron después», señalaba, como si no fuera una hazaña presentar una solución a un problema matemático ante sus pares y consagrarse a los 18 años.
Cursaba su segundo año de carrera universitaria en la Universidad Péter Pázmány de Budapest, y su trabajo era una demostración asombrosamente simple del teorema de Chebyshev, que dice que siempre se puede encontrar un número primo entre cualquier número entero (mayor que 1) y su doble.
Al descubrir una elegante demostración de un famoso teorema de la teoría de números, no sólo había dejado la primera de las que serían cuantiosas huellas en el mundo matemático; también, había logrado algo que sería siempre su aspiración: encontrar, solo o con colegas, las mejores soluciones, «las más simples», de cada problema matemático concebible.
Como muchos matemáticos, creía que las verdades matemáticas se descubren, no se inventan.
Pero, según él, éstas estaban escritas en un libro transfinito («transfinito» es un concepto matemático para algo más grande que el infinito) de teoremas que el S.F. -o el Supremo Fascista, como llamaba a Dios-, y de vez en cuando, si estaba de buen humor o distraído, permitía que los humanos las vieran.

Es por eso que cuando veía algún trabajo matemático que lo impresionaba, expresaba su admiración diciendo: «Viene directamente de El libro».
Nómada matemático
En cuatro años obtuvo no sólo su licenciatura sino también su doctorado en matemáticas de una vez.
Era 1934 y Hungría, con su régimen fascista, se estaba volviendo cada vez más incómodo para los judíos.
Fue entonces que viajó a Inglaterra, para hacer trabajos postdoctorales en Cambridge y Manchester, y descubrió que además de lo que llevaba en una maleta semivacía que nunca aprendió a empacar, no quería más que la oportunidad de ser un turista matemático, viajando a cualquier lugar del mundo en el que estuviera pasando algo interesante y hubiera espacio para pensar y compartir ideas.
Erdős nunca tuvo un empleo formal, una oficina o escritorio. Para hacer su trabajo, sólo necesitaba su mente y, a veces, lápiz y papel.
No tuvo posesiones materiales, pues las consideraba una molestia, ni cuentas de banco, ni tarjetas de crédito.
Tampoco tuvo una relación de pareja ni hijos, aunque le fascinaban los niños a los que llamaba «épsilon», porque pequeñas cantidades en matemáticas a menudo son designadas por esa letra griega.
Y, aparte de la casa de sus padres en Hungría, nunca tuvo un hogar permanente.
En ese viaje de por vida que emprendió siempre en busca de nuevos desafíos, sus amigos, la mayoría matemáticos y eminentes, le daban posada cuando llegaba, usualmente sin avisar, a tocar sus puertas y anunciaba: «Mi mente está abierta».
Sabían que llegaba cargado de ideas y brillantez, de problemas en busca de soluciones y soluciones sin problema, por lo que lo recibían gustosos pese a que estaban conscientes de que les esperaban días de intensas sesiones con alguien cuyo objetivo en la vida era «hacer matemáticas: probar y conjeturar» que jamás aprendió siquiera a cortar en dos la toronja que le gustaba comer al desayuno.